Geant4 무작정 따라하기 - 9. 확률변수 이용하여 선원항 정의하기
Geant4 무작정 따라하기 시리즈의 아홉번째. 확률변수를 이용하여 Event마다 바뀌는 선원항을 정의하는 방법을 알아봅니다.
등방성 점선원 모사
문제 제기
등방적으로 발생하는 점선원을 생각해봅시다. 일반적으로 다음 그림과 같은 모양이 떠오를 것입니다.
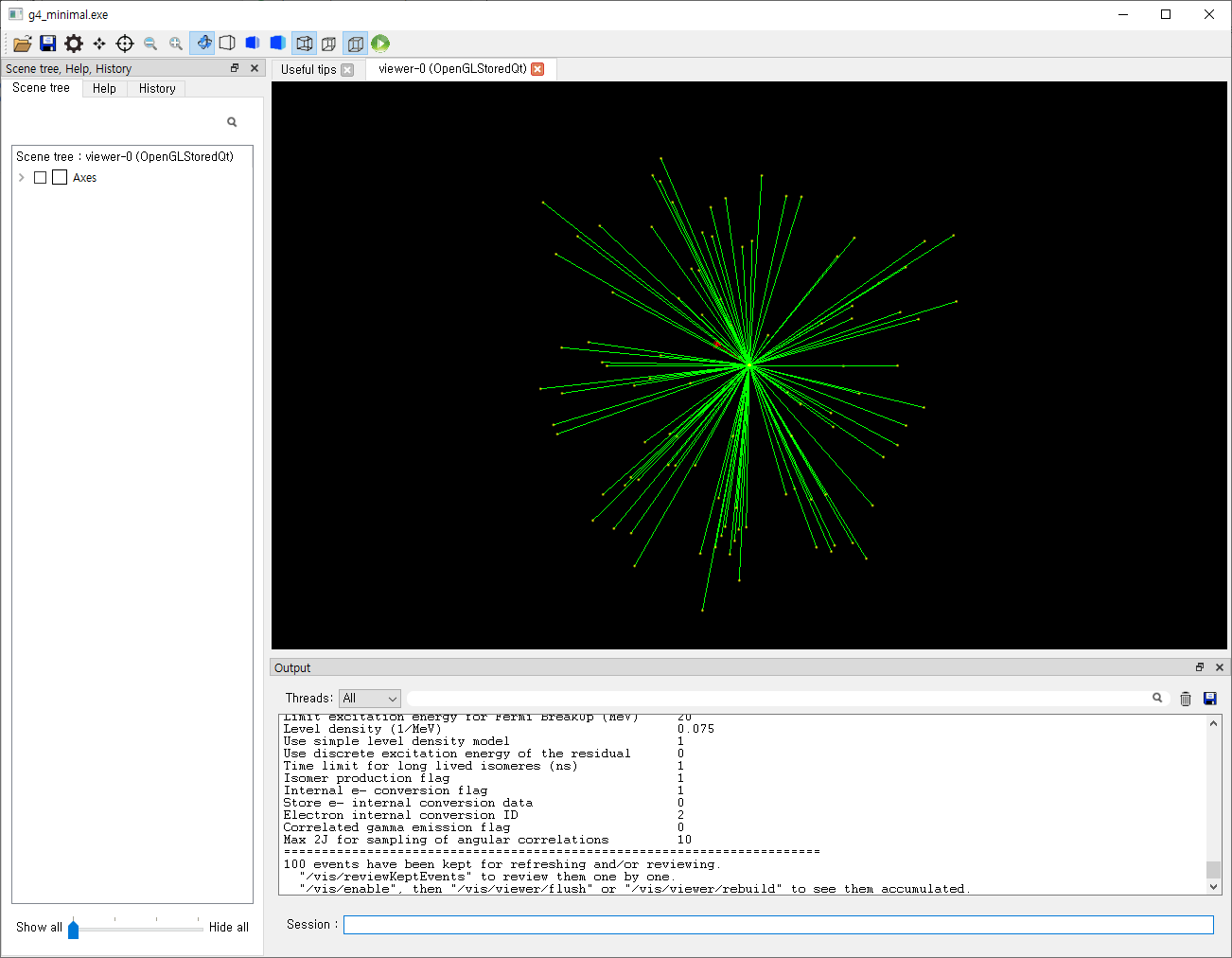
하지만 앞서 말씀드린 것처럼 Geant4는 한 번에 하나의 입자만을 수송하기 때문에, 실제로는 다음과 같이 매 Event마다 방향이 바뀌는 입자가 순차적으로 나오는 형태일 것입니다.
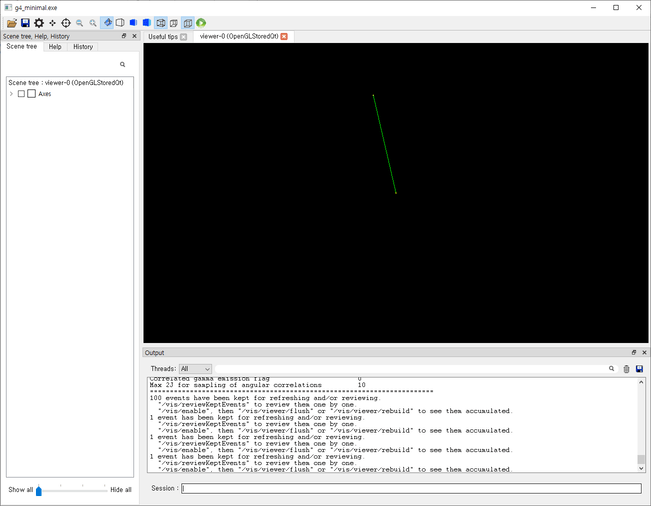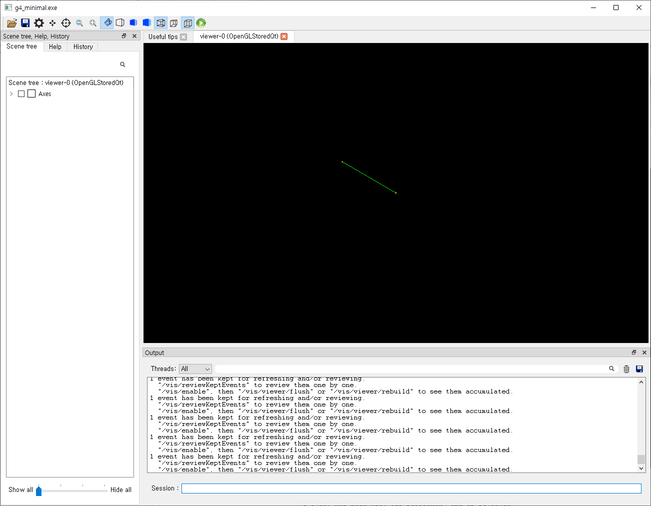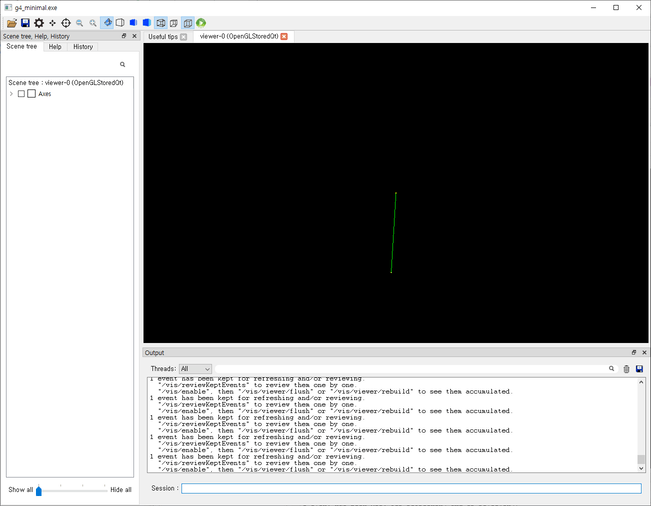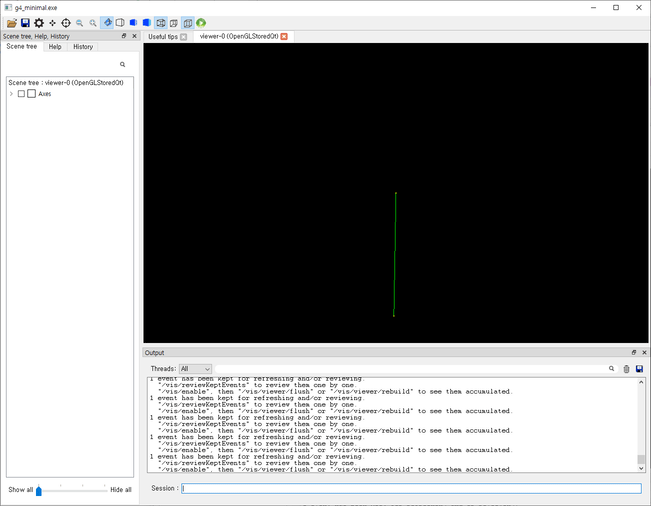
이제 앞서 배운 선원항의 방향 정의 부분을 다시 살펴봅시다.
예를 들어 초기 입자의 운동방향을 +Z축인 (0, 0, 1)으로 설정하고 싶다면, 다음과 같이 입력하면 됩니다.
1 // ... 2 void PrimaryGeneratorAction::GeneratePrimaries(G4Event *anEvent) 3 { 4 // ... 5 fPrimary->SetParticleMomentumDirection(G4ThreeVector(0., 0., 1.)); 6 7 fPrimary->GeneratePrimaryVertex(anEvent); 8}
SetParticleMomentumDirection 함수를 통해 방향을 설정하고, 이 때 방향은 G4ThreeVector 형태로 입력을 해주어야 합니다. 우리는 결국 방향을 명시해서 입력해 줘야만 하는데, 이 방향이 알아서 매 번 바뀌어야 하는 상황에 놓였습니다.
해결책
이 문제를 해결하기 위해 다음과 같은 함수를 상상해봅시다.
-
이 함수는 G4ThreeVector를 반환하는데, 함수가 호출될 때마다 반환되는 값이 매번 바뀝니다.
-
반환되는 G4ThreeVector들을 쭉 모아서 분포를 살펴보니, 단위구(Unit sphere) 표면 위의 점이 균일한 확률로 나옵니다.
-
함수의 원형은 다음과 같습니다.
1G4ThreeVector RandomDirection();
이런 함수를 어떻게 만들 수 있을 지는 나중에 생각해보기로 하고, 이 함수의 출력값을 먼저 살펴봅시다. 아마도 다음과 같이 나타날 것입니다.
1G4ThreeVector dir;
2
3dir = RandomDirection(); // dir = G4ThreeVector(-0.157616,-0.293535,-0.942865);
4dir = RandomDirection(); // dir = G4ThreeVector(0.185649,-0.743512,0.642437);
5dir = RandomDirection(); // dir = G4ThreeVector(0.643525,0.268099,0.716937);
6dir = RandomDirection(); // dir = G4ThreeVector(0.636717,-0.421678,0.645584);
바로 이 RandomDirection() 함수가 바로 우리가 원하던 방향을 등방적으로 균일하게 매 번 알아서 바꾸어서 제공해주는 함수입니다. 이런 함수만 있다면 선원항을 다음과 같이 정의하여 우리의 문제를 해결할 수 있겠군요. 다음과 같이 말입니다.
1// ...
2void PrimaryGeneratorAction::GeneratePrimaries(G4Event *anEvent)
3{
4 // ...
5 auto dir = RandomDirection();
6 fPrimary->SetParticleMomentumDirection(dir);
7
8 fPrimary->GeneratePrimaryVertex(anEvent);
9}
설명
이처럼 특정한 확률분포(Probability Distribution Function, PDF)를 따라 변하는 수를 확률변수라고 합니다. 그리고 이렇게 확률변수를 생성해내는 행위를 샘플링(sampling)한다고 합니다.
확률변수에 있어 가장 기본이 되는 것은, 소위 난수(random number)라고 불리는 $ \xi \sim \mathcal{U}(0,1) $입니다. 0~1 범위 내의 실수가 균일하게 샘플링되는 난수 $ \xi $를 반환하는 함수는 대부분의 프로그래밍 언어가 기본으로 제공하고 있습니다1. 이 $ \xi $만 있으면, 이론상 임의의 PDF를 따르는 확률변수를 샘플링하는 함수를 만들 수 있습니다.
물론 이 부분은 수학적인 기교가 들어가는 내용이므로 여기서 다루지는 않겠습니다.
중요한 점은, 이렇게 확률변수를 샘플링하는 함수만 있으면 매 번 발생 조건이 바뀌는 선원항도 정의할 수 있게 된다는 것입니다.
G4RandomTools.hh
Geant4는 G4RandomTools.hh라는 헤더를 통해, 자주 사용되는 PDF에 대해 확률변수를 샘플링하는 다양한 함수를 이미 만들어서 제공하고 있습니다. 덕분에 이러한 함수를 굳이 공부하여 만들어 쓸 필요가 없습니다.
대표적인 함수들을 일부 소개해드리겠습니다. (10.7 버전 기준)
G4RandomDirection
앞서 설명했던, 등방적으로 방향을 샘플링하는 함수입니다. 원형은 다음과 같습니다.
1G4ThreeVector G4RandomDirection();
2G4ThreeVector G4RandomDirection(G4double cosTheta);
이 함수는 입력인자를 아예 입력하지 않고 사용할 수 있습니다. 이 경우 모든 방향($ 4\pi $)에 대해 균일하게 샘플링된 G4ThreeVector를 반환받을 수 있습니다.
혹은, 입력인자로 임의의 각도 $ \theta $에 대해 $ \mathcal{cos} \theta $ 값에 해당하는 실수(G4double)를 넣을 수도 있습니다. 이 경우에는 $ +z $축을 중심축으로 하고 꼭짓각의 절반이 $ \theta $인 원뿔 형태로 제한된 영역에 대해 균일하게 샘플링된 G4ThreeVector를 반환받을 수 있습니다.
G4LambertianRand
입력된 벡터를 법선벡터로 갖는 평면에 대해 Lambert 코사인 법칙2을 따르게끔 방향을 샘플링하는 함수입니다. 원형은 다음과 같습니다.
1G4ThreeVector G4LambertianRand(const G4ThreeVector& normal);
이 함수는 입력인자로 G4ThreeVector 하나를 넣어줘야 합니다. 그러면 그 벡터를 법선벡터(normal vector)로 갖는 평면을 기준으로 하여 Lambert 코사인 법칙을 따르는 방향을 샘플링하여 G4ThreeVector 형태로 반환해 줍니다.
G4PlaneVectorRand
입력된 벡터를 법선벡터로 갖는 무한 평면상의 점을 샘플링하는 함수입니다. 원형은 다음과 같습니다.
1G4ThreeVector G4PlaneVectorRand(const G4ThreeVector& normal);
이 함수는 입력인자로 G4ThreeVector 하나를 넣어줘야 합니다. 그러면 그 벡터를 법선벡터(normal vector)로 갖는 무한평면 상의 한 지점을 샘플링하여 G4ThreeVector 형태로 반환받을 수 있습니다.
G4RandomRadiusInRing
평면 원 혹은 평면 고리에서 균일한 분포의 점을 샘플링 하기 위한 반경의 샘플링을 수행해주는 함수입니다. 원형은 다음과 같습니다.
1G4double G4RandomRadiusInRing(G4double rmin, G4double rmax);
원이면 rmin을 0으로, rmax를 반지름으로 주면 됩니다. 고리라면 rmin을 내경으로, rmax를 외경으로 주면 됩니다.
G4RandomPointInEllipse
평면 타원 내에서 균일한 분포의 2차원 점을 샘플링하는 함수입니다. 원형은 다음과 같습니다.
1G4TwoVector G4RandomPointInEllipse(G4double a, G4double b);
$ {x^2 \over a^2} + {y^2 \over b^2} = 1 $의 타원의 방정식을 따르는 평면 타원에 대해 $a$, $b$를 입력인자로 넣으면, 타원 내에서 균일한 분포의 2차원 점을 샘플링하여 반환해줍니다. G4TwoVector는 2차원 벡터를 다루는 클래스로, G4ThreeVector와 유사하게 사용하면 됩니다.
G4RandomPointOnEllipse
평면 타원의 원주 위에서 균일한 분포의 2차원 점을 샘플링하는 함수입니다. 원형은 다음과 같습니다.
1G4TwoVector G4RandomPointOnEllipse(G4double a, G4double b);
$ {x^2 \over a^2} + {y^2 \over b^2} = 1 $의 타원의 방정식을 따르는 평면 타원에 대해 $a$, $b$를 입력인자로 넣으면, 타원의 원주 위에서 균일한 분포의 2차원 점을 샘플링하여 반환해줍니다. In과 On의 차이에 주의하세요.
G4RandomPointOnEllipsoid
3차원 타원체의 표면 위에서 균일한 분포의 3차원 점을 샘플링하는 함수입니다. 원형은 다음과 같습니다.
1G4ThreeVector G4RandomPointOnEllipsoid(G4double a, G4double b, G4double c);
$ {x^2 \over a^2} + {y^2 \over b^2} + {z^2 \over c^2} = 1 $의 타원체의 방정식을 따르는 3차원 타원체에 대해 $a$, $b$, $c$를 입력인자로 넣으면, 타원체의 겉표면 위에서 균일한 분포의 3차원 점을 샘플링하여 반환해줍니다.
G4UniformRand
$ X \sim \mathcal{U}(0,1) $를 따르는 실수를 샘플링하는 함수입니다. 원형은 다음과 같습니다.
1double G4UniformRand();
G4RandFlat::shoot
균등분포를 따르는 실수를 샘플링하는 함수입니다. 원형은 다음과 같습니다.
1double shoot(double a, double b); // example: G4RandFlat::shoot(a, b)
$ X \sim \mathcal{U}(a,b) $를 따르는 확률변수 $ X $를 샘플링하는 함수입니다.
G4RandGaussQ::shoot
정규분포를 따르는 실수를 샘플링하는 함수입니다. 원형은 다음과 같습니다.
1double shoot(double mean, double stdDev); // example: G4RandGaussQ::shoot(mean, stdDev)
평균(mean)이 $\mu$이고, 표준편차(stdDev)가 $\sigma$인 $ X \sim \mathcal{N}(\mu , {\sigma}^2) $를 따르는 확률변수 $ X $를 샘플링하는 함수입니다.
G4RandExponential::shoot
지수분포를 따르는 실수를 샘플링하는 함수입니다. 원형은 다음과 같습니다.
1double shoot(double mean); // example: G4RandExponential::shoot(mean)
평균(mean)이 $\lambda$인 $ X \sim Exp(\lambda) $를 따르는 확률변수 $ X $를 샘플링하는 함수입니다.
실제 적용 - 등방성 점선원
이제 맨처음 고민하였던 등방성 점선원을 모사하는 방법을 모두 알아냈습니다.
PrimaryGeneratorAction 코드를 다음과 같이 작성하면 등방성 점선원을 모사할 수 있게 됩니다.
- 헤더 G4RandomTools.hh를 포함
- SetParticleMomentumDirection() 함수의 입력 인자로, G4RandomDirection() 함수의 출력값을 대입
실제 소스코드는 다음과 같이 작성하면 됩니다.
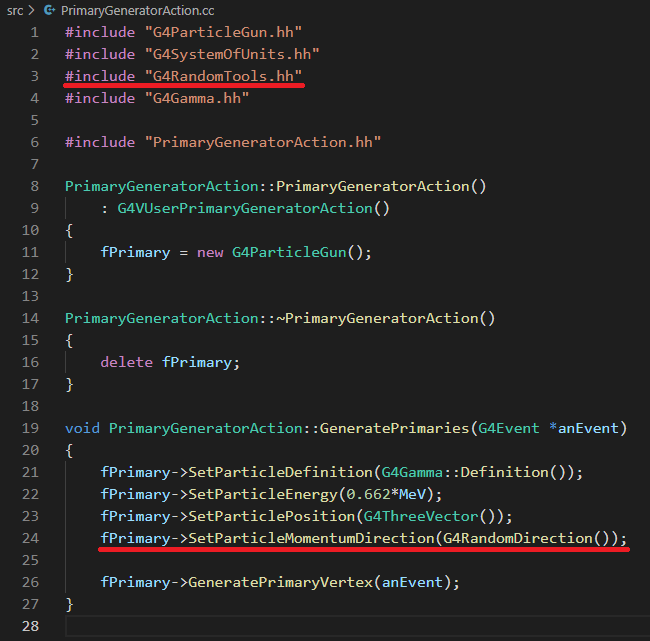
최종 파일 다운받는 법
이번 글에서 작성한 코드는 이 링크를 통해 다운받을 수 있습니다.
혹은 git repository를 clone하신 분의 경우에는, example branch의 이전 커밋 중 V2 PriGen이라는 커밋을 참고하셔도 됩니다.
정리
이로써 선원항을 정의하는 방법까지 마쳤습니다.
다음 글에서는 시뮬레이션을 돌리며 원하는 정보를 획득하는 스코어링에 대해 살펴보도록 하겠습니다.
-
사실 컴퓨터는 완전히 무작위적인 난수를 발생시키지는 못해서 의사난수(pseudo random number)를 샘플링하는 함수들을 제공합니다. ↩︎
-
이상적인 난반사 표면에서 방출되는 선속이 법선벡터로부터 벗어난 각도의 $ \mathcal{cos} $ 값에 비례한다는 법칙. 참고 링크: Lambert’s cosine law - Wikipedia ↩︎